Homemade Diddley Bow
We began our second unit of Light, Sound and Time by discussing what sound is. We compared it with noise and silence, differentiating the definitions by opinion. The research moved on to how our ear processes sound waves, its anatomy, and the speed of sound. We differentiated a traveling wave versus a standing wave, and incorporated physics into our calculations using sine, cosine, and functions. We revisited Chicago Music Exchange to learn about the details of how synthesizers, amplifiers, guitars, and drums work. Some important concepts our class dwelled on were:
Pitch, being the frequency of a sound wave, regulating how high or low it is.
Amplitude, being the loudness of sound represented by the height of crest to valley in a sound wave.
And The Doppler Effect, which happens when sound travels past you, and waves are compressed in the front, creating a high pitch. Then as it travels farther the waves widen at the rear, creating a low pitch. The nearer the sound is, the higher the pitch.
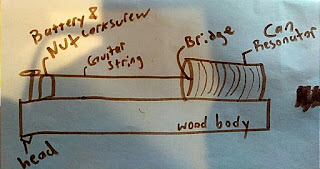
Our Action project had us build a homemade Diddley Bow out of a plank of wood, a guitar string, screws, a can, corkscrews, and batteries. The purpose was not only for the experience of Doing It Yourself, but to show how materials and objects can be recycled into nearly anything. It represents sustainability and taking advantage of what's already been made to sustain a closed loop system, like in our Bio mimicry unit. Here I present a sketch of my Diddley Bow:
Our Action project had us build a homemade Diddley Bow out of a plank of wood, a guitar string, screws, a can, corkscrews, and batteries. The purpose was not only for the experience of Doing It Yourself, but to show how materials and objects can be recycled into nearly anything. It represents sustainability and taking advantage of what's already been made to sustain a closed loop system, like in our Bio mimicry unit. Here I present a sketch of my Diddley Bow:
This is how my Diddley Bow turned out:
On the neck of my instrument I labeled its harmonics. The harmonics represent the overtone of a strummed note. Each level represents a series of harmonics that vibrate when that note is played:
Thickness of string: 0.02 in
All in all, this project tested my patience as I built the instrument. However, the work held purpose and taught me the details of sound's functions. I present to you a recording of me playing my Diddley Bow.
 |
| Homemade Diddley Bow, PKA, 2019 |
On the neck of my instrument I labeled its harmonics. The harmonics represent the overtone of a strummed note. Each level represents a series of harmonics that vibrate when that note is played:
 |
| Harmonics, PKA, 2019 |
The Diddley Bow string is in a state of tension between the nut (at the corkscrew) and behind the can, which acts as a resonator. When you pluck the string, it vibrates within and its pitch resonates.
Thickness of string: 0.02 in
Length of String Vibration: 15.125 in
I calculated the angle (81.9 degrees) of the string from the nut to the can since it is not exactly parallel to the wood length. The string was longer than the wood by 0.125 inches:
I calculated the volume of my can:
These are my calculations for Frequency, Wavelength, and Harmonics:
 |
| Calculations, PKA, 2019 |


Comments
Post a Comment